You can also use the and keys
| | Additions are marked like this |
In hyperbolic geometry, the horocyclic flow on a hyperbolic surface is a canonical flow on the unit tangent bundle of the surface that moves tangent vectors sideways along the horocycle centered in the tangent vector's direction. | In hyperbolic geometry, the horocyclic flow on a hyperbolic surface is a canonical flow on the unit tangent bundle of the surface that moves tangent vectors sideways along the horocycle centered in the tangent vector's direction. 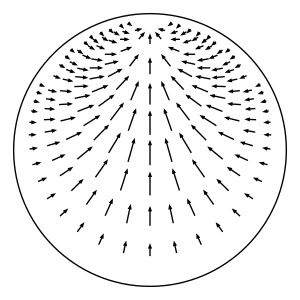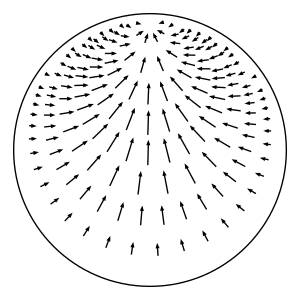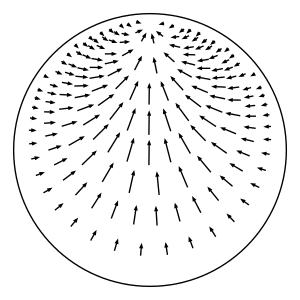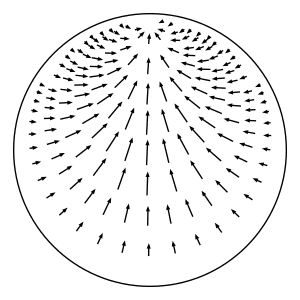
|