| | Additions are marked like this |
In hyperbolic geometry, the horocyclic flow on a hyperbolic surface is a canonical flow on the unit tangent bundle of the surface that moves tangent vectors sideways along the horocycle whose center is in the direction of the tangent vector. DefinitionMore precisely, let \(S\) be a complete oriented hyperbolic surface, and let \(T^1(S)\) denote the unit tangent bundle of \(S\). Consider a point \(p = (x, v)\in T^1(S)\), where \(x\in S\) and \(v\) is a unit tangent vector based at \(x\). We define the horocyclic flow by describing where the flow takes \(p\) at time \(t\in \mathbb{R}\). We use \(h\) to denote the horocyclic flow on \(S\), and we let \(h_t: T^1(S)\to T^1(S)\) denote the mapping at time \(t\). 
As shown in the figure above, lift \(p\) to a point \(\widetilde{p} = (\widetilde{x}, \widetilde{v})\) in the unit tangent bundle of the hyperbolic plane \(\mathbb{H}\). (The hyperbolic plane is the universal cover of \(S\).) Let \(c\) denote the point in the boundary at infinity of \(\mathbb{H}\) that \(\widetilde{p}\) points to. In other words, the point \(c\) is the endpoint of the geodesic ray that starts at \(\widetilde{x}\) and whose tangent vector is \(\widetilde{v}\). Consider the oriented horocycle \(C\) in \(\mathbb{H}\) with center \(c\) and that passes through \(\widetilde{x}\) from left to right when facing in the direction of \(\widetilde{v}\). (This is where we use the orientation of \(S\).) Define \(\widetilde{p}_t\) to be the element \((\widetilde{x}_t, \widetilde{v}_t)\in T^1(\mathbb{H})\), where \(\widetilde{x}_t\) is the result of moving \(\widetilde{x}\) along \(C\) for time \(t\) at unit speed (measuring distance relative to the metric that \(C\) inherits from \(\mathbb{H}\)), and \(\widetilde{v}_t\) is the unit tangent vector based at \(\widetilde{x}_t\) pointing towards the same boundary point \(c\). Note that the distance between \(\widetilde{x}_t\) and \(\widetilde{x}\) as measured in \(\mathbb{H}\) will be strictly less than \(t\) because \(C\) is not a geodesic. (This distance in \(\mathbb{H}\) is \(2\sinh^{-1}(t / 2) < t\).) Project \(\widetilde{p}_t\) down to \(p_t\in T^1(S)\) to get \(h_t(p)\). This defines a well-defined flow because the construction doesn't depend on the choice of lift nor on the time \(t\). 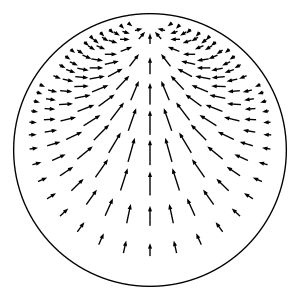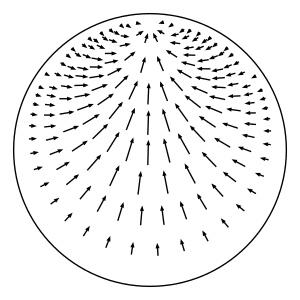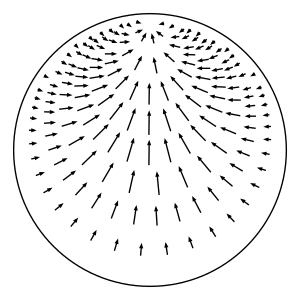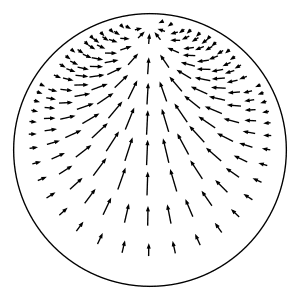
| In hyperbolic geometry, the horocyclic flow on a hyperbolic surface is a canonical flow on the unit tangent bundle of the surface that moves tangent vectors sideways along the horocycle whose center is in the direction of the tangent vector. DefinitionMore precisely, let \(S\) be a complete oriented hyperbolic surface, and let \(T^1(S)\) denote the unit tangent bundle of \(S\). Consider a point \(p = (x, v)\in T^1(S)\), where \(x\in S\) and \(v\) is a unit tangent vector based at \(x\). We define the horocyclic flow by describing where the flow takes \(p\) at time \(t\in \mathbb{R}\). We use \(h\) to denote the horocyclic flow on \(S\), and we let \(h_t: T^1(S)\to T^1(S)\) denote the mapping at time \(t\). 
As shown in the figure above, lift \(p\) to a point \(\widetilde{p} = (\widetilde{x}, \widetilde{v})\) in the unit tangent bundle of the hyperbolic plane \(\mathbb{H}\). (The hyperbolic plane is the universal cover of \(S\).) Let \(c\) denote the point in the boundary at infinity of \(\mathbb{H}\) that \(\widetilde{p}\) points to. In other words, the point \(c\) is the endpoint of the geodesic ray that starts at \(\widetilde{x}\) and whose tangent vector is \(\widetilde{v}\). Consider the oriented horocycle \(C\) in \(\mathbb{H}\) with center \(c\) and that passes through \(\widetilde{x}\) from left to right when facing in the direction of \(\widetilde{v}\). (This is where we use the orientation of \(S\).) Define \(\widetilde{p}_t\) to be the element \((\widetilde{x}_t, \widetilde{v}_t)\in T^1(\mathbb{H})\), where \(\widetilde{x}_t\) is the result of moving \(\widetilde{x}\) along \(C\) for time \(t\) at unit speed (measuring distance relative to the metric that \(C\) inherits from \(\mathbb{H}\)), and \(\widetilde{v}_t\) is the unit tangent vector based at \(\widetilde{x}_t\) pointing towards the same boundary point \(c\). Note that the distance between \(\widetilde{x}_t\) and \(\widetilde{x}\) as measured in \(\mathbb{H}\) will be strictly less than \(t\) because \(C\) is not a geodesic. (This distance in \(\mathbb{H}\) is \(2\sinh^{-1}(t / 2) < t\).) Project \(\widetilde{p}_t\) down to \(p_t\in T^1(S)\) to get \(h_t(p)\). This defines a well-defined flow because the construction doesn't depend on the choice of lift nor on the time \(t\). 
|
You can also use the and keys